Innovation: Improving ARAIM

An approach using precise point positioning

By R. Eric Phelts, Kazuma Gunning, Juan Blanch and Todd Walter

Innovation Insights with Richard Langley

AS WE NOTED IN THE LAST INNOVATION COLUMN, integrity — at least from a safety viewpoint — is the most important characteristic of a navigation system. Yes, accuracy, availability and continuity are also required but, without integrity, the advertised accuracy of a system might become meaningless and perhaps misleading. While GPS and user receivers are highly reliable, we cannot presume that there will never be an erroneous signal transmitted by a GPS satellite that would result in a receiver outputting a hazardously misleading position solution. While “supervisory” systems such as satellite-based augmentation systems monitor GPS signals and can alert users about defective satellites within a very short period of time, it is advantageous for a user receiver to autonomously detect problematic satellites and quarantine them so that they do not perturb the position solution.

It is for this reason that receiver autonomous integrity monitoring (RAIM) techniques were developed. As we know, a receiver needs signals from a minimum of four satellites simultaneously to determine its 3D position and its clock offset. However, typically there are more than four satellites in view, and so multiple solutions using subsets of four satellites are possible. If five satellites are visible, then it is possible to determine that one of them is faulty, but not which one (geometry plays a role here). This is called fault detection (FD). And if six satellites are visible, the faulty satellite can be determined and then excluded from the position solution (fault detection and exclusion, or FDE). This is the basic principle of RAIM.

Advanced RAIM (ARAIM) extends RAIM to other constellations beyond GPS. ARAIM enables the use of the newer GNSS constellations to provide better levels of performance than RAIM with GPS alone. It also uses dual-frequency measurements for enhanced vertical positioning reliability.

Central to positioning techniques providing a safety-of-life service is the notion that the uncertainty of a provided position must be conservatively estimated and provide for both nominal uncertainty and the uncertainty of a faulted solution such as that detected using RAIM. These conservative estimates are known as the horizontal and vertical protection levels. The horizontal protection level (HPL) is the radius of a circle in the horizontal plane with its center at the true position, which describes the region that is assured to contain or bound the provided horizontal position to a very high probability. The vertical protection level is half the length of a segment in the vertical direction with its center at the true position, which describes the region that is assured to contain or bound the provided vertical position to a very high probability. The probability levels are typically taken to be 99.9999998 and 99.99999% for HPL and VPL, respectively.

The usual approach for RAIM and ARAIM is to use the so-called “snapshot” approach, where measurements are assumed to be uncorrelated epoch to epoch. In this month’s column, a team of authors from Stanford University discusses a superior approach for ARAIM using the technique of precise point positioning.

Advanced Receiver Autonomous Integrity Monitoring (ARAIM) is implemented using solution separation in positioning and navigation software. Solution separation computations presume one or more GNSS satellites may be faulty, and they iteratively compute multiple position solutions comprised of subsets of the n satellites in view (n, n-1, n-2, and so on) to ensure that at least one of the solutions is fault-free. Using assumptions on the nominal and faulted uncertainty of the solutions, the software can compute conservative horizontal and vertical protection levels (PLs) by bounding the uncertainty from all the solutions. This assures (to a targeted level of probability) that the user position is contained within these limits.

Traditional solution separation techniques generally operate as a “snapshot.” The basic measurements are dual-frequency, carrier-smoothed pseudorange (code), and errors are generally assumed to be uncorrelated from epoch to epoch. This procedure requires that errors at each time step are conservatively bounded with large uncertainties (sigmas) designed to protect the user against the worst-case error. These assumptions minimize the complexity and computational cost of the solution by providing a robust, provably safe bound. However, the PLs computed are relatively large. In addition, they can change suddenly from one epoch to the next due to changes in available satellites or platform dynamics. This can make meeting performance goals (such as continuity) for aircraft approaches more challenging.

Solution separation procedures using techniques based on precise point positioning (PPP) implement an extended Kalman filter (EKF) to filter measurements over time. In this case, the basic measurements are dual-frequency code and carrier phase, and errors are assumed to have some correlation between each time step to the next. Accordingly, these techniques leverage higher quality measurements (that is, carrier-phase-based as opposed to code-based) to smooth and reduce large sigmas and to estimate (and calibrate) errors over time. The complexity associated with defining and characterizing the decorrelation models for the errors, so that the nominal covariance produced by the EKF conservatively describes the actual error, is significant. Also, the computational cost of estimating the error states may be substantially higher than with the traditional snapshot approach. However, the computed protection levels provide integrity and are often significantly smaller. In addition, the filtering makes them more robust to platform dynamics, which makes them well-suited for aircraft in flight.

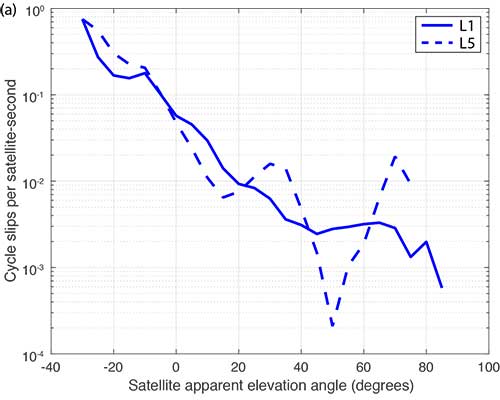
Flight Data: Outages and Cycle Slips. ARAIM performance may be significantly affected by aircraft dynamics. Specifically, banking can induce satellite outages and cycle slips. Outages weaken the constellation geometry and can cause sudden changes in the protection level. Frequent cycle slips prevent code measurements from being smoothed, potentially inflating protection levels of carrier-phase-smoothed code measurements for extended periods of time.

When the outages and cycle slips are computed as a rate, a trend can be seen. Both increase notably as the relative elevation angle to the satellites decrease. FIGURE 1 shows an example of outages as a function of the apparent elevation angle of the satellites (relative to the aircraft). Cycle slips on GPS L1-L5 and Galileo El-E5a are plotted in FIGURES 2 (a) and (b), respectively.

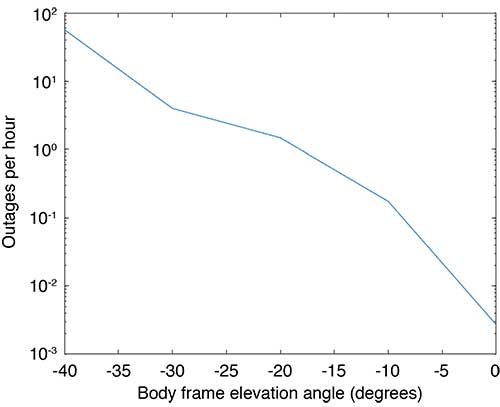
FIGURE 1. Outages as a function of body frame or apparent elevation angle during aircraft banking. (Image: Authors)

FIGURE 2a. Cycle-slip rate (per satellite-second) for GPS L1-L5. (Image: Authors)

FIGURE 2b. Cycle-slip rate (per satellite-second) for E1-E5a. (Image: Authors)

For this article, we have used the flight data from one of our earlier papers on the effect of aircraft banking on ARAIM performance (see Further Reading). With this data, we show that significant advantages of PPP can be retained even during aircraft maneuvers when outages and cycle slips threaten ARAIM continuity and availability the most.

MODEL ASSUMPTIONS

The traditional snapshot solution separation approach is well-established and was implemented according to the standards established by a working group operating under the U.S.-European Union Agreement on GPS-Galileo Cooperation, which has been extended to all constellations (see Further Reading). For this article, we limited the constellations to GPS and Galileo, and the prior probabilities assumed for satellite and constellation faults were as follows:

P_sat = 10^-5, P_const,GPS = 10^-8 and P_const,GAL = 10^-4

We implemented the PPP algorithm with solution separation using an EKF using dual-frequency code and carrier-phase measurements (from GPS and Galileo) with estimated parameters comprising the receiver position and velocity, clock biases for each constellation in use, a residual tropospheric delay, carrier-phase float ambiguities for each tracked carrier, multipath error, receiver differential code bias, and broadcast orbit and clock error. Modeled (not estimated) effects include solid Earth tide modeling, ocean loading, an initial tropospheric delay and relativistic effects. Many of the details of the implementation can be found in our paper “Design and Evaluation of Integrity Algorithms for PPP in Kinematic Applications” (see Further Reading).

PPP techniques typically utilize precise ephemeris information obtained from a global network of ground reference stations such as those operating in the network coordinated by the International GNSS Service. Snapshot solution separation techniques, however, use only ephemeris information broadcast from the satellites themselves. For a proper comparison of the protection levels computed by each technique, the PPP filter was constrained to use this broadcast information.

The model we have applied is mostly typical of a traditional PPP implementation with one significant exception — the state tracking the error contribution of the broadcast orbit and clock on each line-of-sight signal. The error contributed by the broadcast orbit and clock is handled by the filter leveraging a characterization of the rate of change of the error, then including it as an estimation state for each line of sight and only adding enough process noise to capture the slowly changing error. We have previously characterized the rate of change of the error in the broadcast orbit and clock and process noise (for GPS). Complete tables of initial state uncertainties and additional settings for process and measurement noise were provided in our earlier work (see Further Reading).

RESULTS

Flight data collected over a period of approximately one year was used to evaluate ARAIM performance through momentary outages and cycle slips due to aircraft dynamics. A multi-constellation, multi-frequency receiver tracked GPS (L1 C/A and L5) and Galileo (E1 and E5a) satellites. This receiver is installed in a Global 5000 jet owned and operated by the FAA William J. Hughes Technical Center. It records and stores GNSS measurements whenever flights are taken. The data we used for this article included data recorded over approximately 35 flights from September 2017 to April 2018.

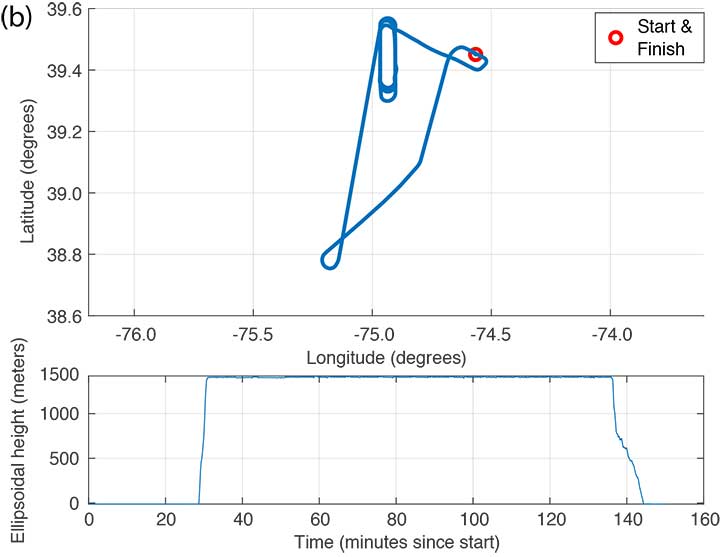
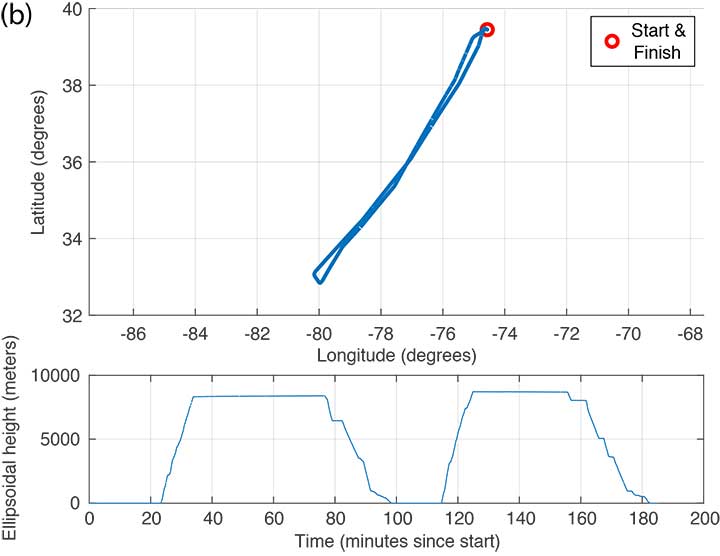
FIGURE 3 shows the trajectory and altitude information corresponding to a single flight (Flight #6) taken on Sept. 20, 2017, and FIGURE 4 compares the corresponding horizontal and vertical protection levels computed using snapshot and “broadcast” PPP techniques. For an additional reference, we also computed protection levels using PPP with precise orbits and clocks (we call this precise PPP despite the terminology redundancy) and plotted these in Figure 4, too.

FIGURE 3b. Altitude information for Flight #6 (Sept. 20, 2017). (Image: Authors)

FIGURE 4a. Horizontal protection levels for Flight #6 (Sept. 20, 2017); red circles indicate a satellite being dropped or reentering the solution. (Image: Authors)

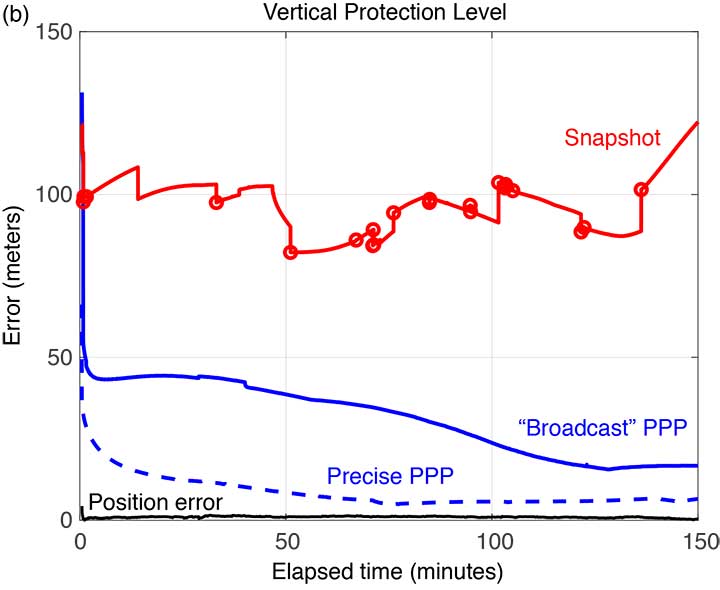
FIGURE 4b. Vertical protection levels for Flight #6 (Sept. 20, 2017); red circles indicate a satellite being dropped or reentering the solution. (Image: Authors)

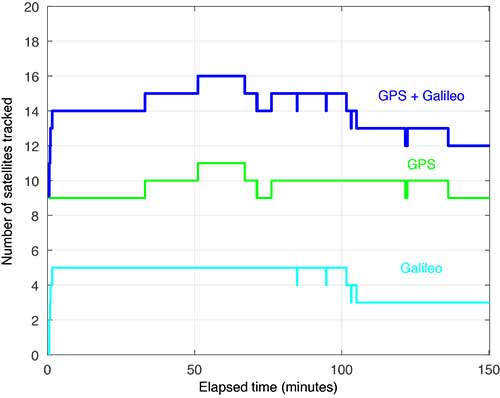
Several things are readily apparent from these comparisons. First, after the initial time required for convergence, there is a substantial reduction in the PLs using the broadcast-PPP-based approach. The precise PPP PLs, as expected, produce the largest reduction, but use additional information not available to the snapshot method. In addition, the snapshot solution separation PLs vary significantly due to cycle slips and momentary satellite outages. FIGURE 5 shows the number of satellites tracked by the receiver during this flight; red circles plotted on the snapshot protection-level line indicate when satellites are coming into and out of view. Despite numerous abrupt changes in number of measurements and measurement quality, the EKF of the PPP techniques produces PLs that are relatively smooth and continuous.

FIGURE 5. Number of satellites tracked for Flight #6 (Sept. 20, 2017). (Image: Authors)

FIGURE 6 shows the trajectory and altitude information corresponding to Flight #4 taken on Sept. 15, 2017.

FIGURE 6a. Flight path for Flight #4 (Sept. 20, 2017). (Image: Authors)

FIGURE 6b. Altitude information for Flight #4 (Sept. 20, 2017). (Image: Authors)

FIGURE 7 compares the horizontal and vertical PLs for snapshot solution separation and the PPP-based techniques.

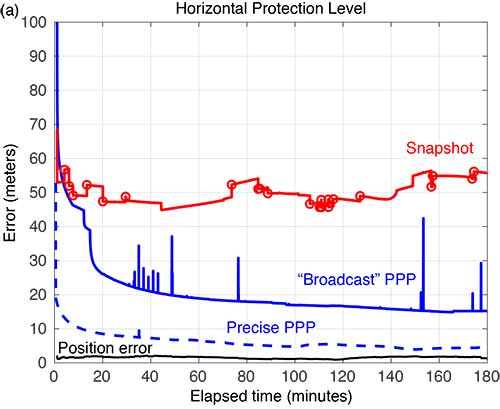
FIGURE 7. Horizontal protection levels for Flight #4 (Sept. 15, 2017); red circles indicate a satellite being dropped or reentering the solution. (Image: Authors)

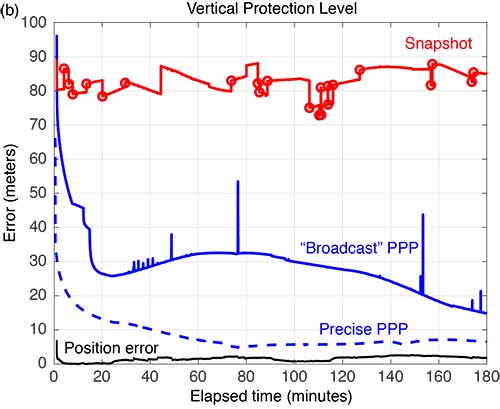
FIGURE 7b. Vertical protection levels for Flight #4 (Sept. 15, 2017); red circles indicate a satellite being dropped or reentering the solution.

As in the case shown in Figure 4, the PLs in Figure 7 reveal a substantial reduction in the mean PLs computed using the PPP-based approach. And the snapshot solution separation approach displays even more variations due to momentary satellite outages. Some of the cycle slips affected enough satellites to introduce brief spikes in the PPP solution as well. These reconverge quickly, but they suggest that some tuning of the EKF can still be done to mitigate these interruptions. Still, the filtered approach produces PLs that are more robust to the outages and are substantially smaller than with the snapshot method.

FIGURE 8 compares the horizontal and vertical PLs computed using snapshot solution separation and PPP techniques for Flight #20 — where the airplane remained stationary on the runway. In the absence of flight dynamics, the levels for all the approaches were relatively smooth. However, a few discontinuities can still be observed for the snapshot case. Also note, in the case of the broadcast PPP, the convergence time is noticeably longer. This is likely because the integer ambiguity resolution in the solution took longer to converge without platform motion.

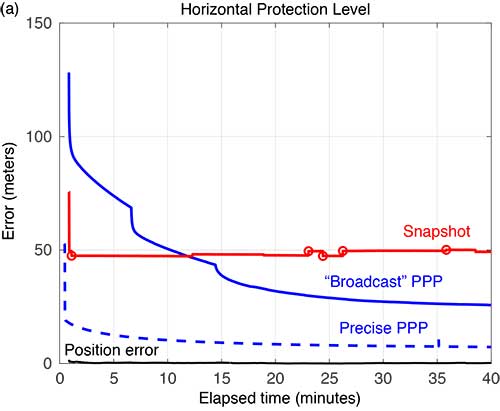
FIGURE 8a. Horizonta protection levels for a stationary aircraft (Flight #20, Dec. 4, 2017); red circles indicate a satellite being dropped or reentering the solution. (Image: Authors)

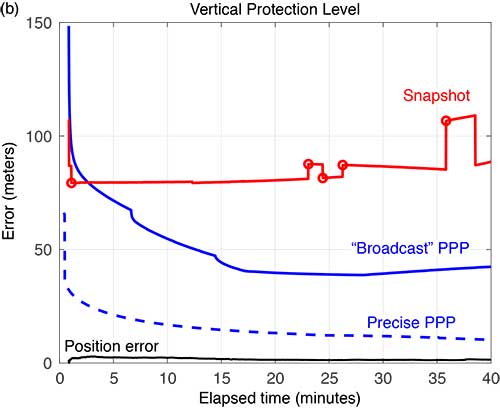
FIGURE 8b. Vertical protection levels for a stationary aircraft (Flight #20, Dec. 4, 2017); red circles indicate a satellite being dropped or reentering the solution. (Image: Authors)

The mean horizontal and vertical PLs for both techniques are summarized in FIGURE 9. (There were issues with the data from Flight #14 and it was not processed.) The PPP approach consistently produces protection levels anywhere from 30 to 75% smaller than those computed using the snapshot approach. The mean PLs for the PPP techniques were always below those computed with the snapshot method.

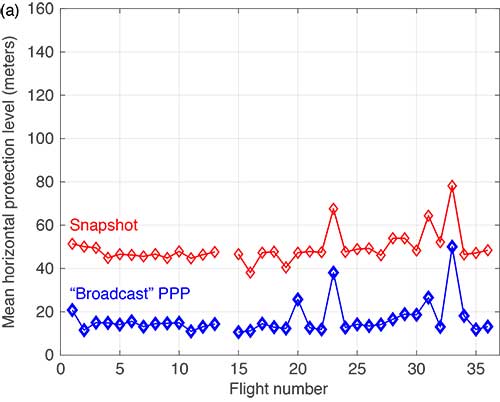
FIGURE 9a. Comparison of mean horizontal PLs for “snapshot” vs. a PPP-based technique. (Image: Authors)

FIGURE 9b. Comparison of mean vertical PLs for “snapshot” vs. a PPP-based technique. (Image: Authors)

CONCLUSIONS

Data from 35 flights was used to compare ARAIM protection levels computed by the traditional “snapshot” solution separation versus a PPP-based approach during both in-flight and several static scenarios. We observed that the filtering of PPP methods yields mean PLs approximately 30 to 75% of those computed using traditional methods in all cases. This improvement can be attributed to exploiting — through filtering and estimation — carrier-phase-based measurements and a time-correlation of the errors. In addition, the EKF employed by the PPP approach demonstrated improved robustness to outages and cycle slips induced by aircraft dynamics. Despite the increased complexity and computational cost, we believe that PPP approaches hold promise for significantly improving ARAIM performance.

ACKNOWLEDGMENT

This article is based on the paper “Evaluating the Application of PPP Techniques to ARAIM Using Flight Data” presented at ION ITM 2020, the 2020 International Technical Meeting of The Institute of Navigation, San Diego, California, Jan. 21–25, 2020.

MANUFACTURER

The flight data was recorded using a Trimble BX935-INS receiver fed by an Antcom Avionic II GNSS antenna.

R. ERIC PHELTS is a research associate in the Department of Aeronautics and Astronautics at Stanford University, California. He received a Ph.D. in mechanical engineering from Stanford University in 2001. His research involves signal deformation monitoring for SBAS and flight-data analyses for ARAIM.

KAZUMA (KAZ) GUNNING is a Ph.D. candidate in the GPS Laboratory at Stanford University working under the guidance of Todd Walter. He is also the navigation algorithms and architecture lead at Xona Space Systems in San Mateo, California. His research interests are in precise point positioning and integrity.

JUAN BLANCH is a senior research engineer at Stanford University, where he works on integrity monitoring algorithms for radionavigation. He received a Ph.D. in aeronautics and astronautics from Stanford University in 2003. He has received The Institute of Navigation (ION) Parkinson and Early Achievement awards.

TODD WALTER is a research professor in the Department of Aeronautics and Astronautics at Stanford University. He received his Ph.D. in applied physics from Stanford University in 1993. His research focuses on implementing high-integrity air navigation systems. He has received the ION Thurlow and Johannes Kepler awards. Walter is also a Fellow of the ION and has served as its president.

Innovation: Improving ARAIM